Stochastik Übungen: Effektives Training für Schüler und Studenten
Einleitung
Was ist Stochastik?
Die Stochastik ist ein zentraler Bestandteil der Mathematik, der sich mit der Analyse von Zufallsprozessen und der Wahrscheinlichkeit von Ereignissen beschäftigt. Sie umfasst die Wahrscheinlichkeitstheorie und die Statistik und wird in vielen Bereichen der Wissenschaft und des täglichen Lebens angewendet. Der Begriff „Stochastik“ leitet sich vom griechischen Wort „stochos“ ab, was „Ziel“ oder „Vermutung“ bedeutet – eine treffende Bezeichnung, da die Stochastik oft dazu verwendet wird, Vorhersagen und Schätzungen zu treffen. Sie hilft uns, mit Unsicherheit umzugehen und zu bestimmen, wie wahrscheinlich es ist, dass bestimmte Ereignisse eintreten.
Die Stochastik ist nicht nur ein abstraktes Konzept der Mathematik, sondern hat viele praktische Anwendungen. Sie spielt eine zentrale Rolle in der Wirtschaft, bei der Risikoanalyse und in der Medizin, insbesondere bei der Bestimmung von Wahrscheinlichkeiten für Krankheitsverläufe. In diesem Artikel werden wir die Grundlagen, Methoden und Anwendungen der Stochastik detailliert beleuchten, um zu zeigen, wie sie die Welt um uns herum beeinflusst.
Warum ist Stochastik wichtig?
Die Stochastik ist nicht nur für Mathematiker und Statistiker von Bedeutung, sondern auch für jeden, der in einem Bereich arbeitet, in dem Unsicherheit und Wahrscheinlichkeit eine Rolle spielen. Ob in der Wirtschaft, der Forschung, der Politik oder im Alltag – Entscheidungen basieren oft auf Wahrscheinlichkeiten und stochastischen Modellen. Beispielsweise ist die Finanzmarktanalyse ohne stochastische Modelle kaum vorstellbar, da Anleger ständig mit Unsicherheiten und Risiken umgehen müssen. In der Medizin hilft die Stochastik, die Wirksamkeit von Behandlungen anhand von Wahrscheinlichkeitsmodellen zu bestimmen.
Ein weiteres Beispiel für die Bedeutung der Stochastik zeigt sich in der modernen Technologie, wo sie eine wichtige Rolle in der Datenwissenschaft, der künstlichen Intelligenz und der maschinellen Lernverfahren spielt. So sind etwa die Algorithmen, die hinter Empfehlungssystemen von Streaming-Diensten oder Online-Shops stecken, auf stochastischen Prinzipien aufgebaut, die es ermöglichen, Vorhersagen über das Verhalten von Nutzern zu treffen. Durch das Verständnis der Stochastik können wir diese Unsicherheiten gezielt nutzen, um fundierte Entscheidungen zu treffen.
Grundlagen der Stochastik
Geschichte der Stochastik
Die Entwicklung der Stochastik reicht bis ins 17. Jahrhundert zurück, als bedeutende Mathematiker wie Blaise Pascal und Pierre de Fermat erste Ansätze zur Wahrscheinlichkeitstheorie entwickelten. Diese Pioniere legten den Grundstein für die moderne Stochastik, indem sie das Konzept der Wahrscheinlichkeit als mathematisch handhabbare Größe einführten. Der Ursprung der Stochastik als Disziplin ist eng mit den Glücksspielproblemen verbunden, da die Mathematiker dieser Zeit versuchten, den Ausgang von Würfeln, Karten und anderen Zufallsexperimenten zu berechnen.
Ein weiterer Meilenstein in der Geschichte der Stochastik war die Arbeit von Andrey Kolmogorov in den 1930er Jahren, der das Axiomensystem der Wahrscheinlichkeitstheorie formulierte. Kolmogorov’s Arbeit brachte die Stochastik auf eine fundierte mathematische Basis und legte die Grundlage für viele der heutigen Konzepte, die in der Wahrscheinlichkeitstheorie verwendet werden. Seitdem hat sich die Stochastik kontinuierlich weiterentwickelt und wird heute in einer Vielzahl von Disziplinen genutzt.
Grundbegriffe der Stochastik
Die Stochastik umfasst eine Vielzahl grundlegender Konzepte, die miteinander verknüpft sind. Die wichtigste Grundlage bildet die Zufallsvariable, die den Ausgang eines Zufallsexperiments beschreibt. Zufallsvariablen können diskret oder stetig sein, wobei diskrete Zufallsvariablen nur endlich viele oder abzählbar unendliche Werte annehmen können, während stetige Zufallsvariablen Werte in einem kontinuierlichen Bereich annehmen.
Ein weiteres zentrales Konzept in der Stochastik ist die Wahrscheinlichkeit, die angibt, wie wahrscheinlich es ist, dass ein bestimmtes Ereignis eintritt. Eine Wahrscheinlichkeit wird immer zwischen 0 und 1 angegeben, wobei 0 für ein unmögliches Ereignis und 1 für ein sicheres Ereignis steht. Die Wahrscheinlichkeitstheorie nutzt Wahrscheinlichkeitsverteilungen, um die Verteilung von Zufallsvariablen zu beschreiben, und legt fest, wie diese Wahrscheinlichkeiten auf verschiedene Ereignisse verteilt sind.
Axiomatischer Aufbau der Wahrscheinlichkeitstheorie
Die Wahrscheinlichkeitstheorie wurde in den 1930er Jahren von Andrey Kolmogorov auf eine axiomatische Grundlage gestellt. Das bedeutet, dass die Wahrscheinlichkeit als eine Funktion definiert wurde, die bestimmten Axiomen folgt. Kolmogorovs Axiome der Wahrscheinlichkeit sind:
- Die Wahrscheinlichkeit eines jeden Ereignisses ist eine Zahl zwischen 0 und 1.
- Die Wahrscheinlichkeit des sicheren Ereignisses (des gesamten Ergebnisraums) ist 1.
- Für zwei sich gegenseitig ausschließende Ereignisse ist die Wahrscheinlichkeit ihres Eintretens gleich der Summe der Wahrscheinlichkeiten der einzelnen Ereignisse.
Diese Axiome bilden das Fundament der modernen Wahrscheinlichkeitstheorie und ermöglichen es, eine Vielzahl von komplexen stochastischen Prozessen zu modellieren.
Methoden und Werkzeuge der Stochastik
Kombinatorik
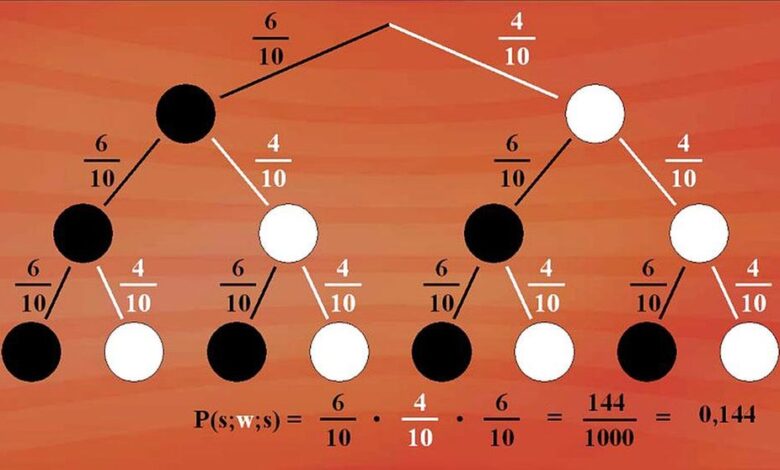
Die Kombinatorik ist ein Teilbereich der Mathematik, der sich mit der Zählung von möglichen Anordnungen und Kombinationen von Objekten befasst. In der Stochastik wird die Kombinatorik oft verwendet, um die Anzahl möglicher Ereignisse zu berechnen und Wahrscheinlichkeiten abzuschätzen. Ein einfaches Beispiel ist das Werfen eines Würfels, bei dem es sechs mögliche Ergebnisse gibt. Die Kombinatorik hilft, alle möglichen Kombinationen und Permutationen zu zählen, was für die Berechnung von Wahrscheinlichkeiten entscheidend ist.
Ein weiteres Beispiel ist die Berechnung der Wahrscheinlichkeit, dass in einer Lotterie ein bestimmtes Gewinnlos gezogen wird. Hier kommt die Kombinatorik ins Spiel, da man die Gesamtzahl der möglichen Loskombinationen und die Anzahl der Gewinnmöglichkeiten berücksichtigen muss, um die Wahrscheinlichkeit eines Gewinns zu berechnen.
Erwartungswert und Varianz
Der Erwartungswert (auch Mittelwert genannt) einer Zufallsvariablen ist der theoretische Durchschnittswert, den man erwarten würde, wenn ein Zufallsexperiment unendlich oft wiederholt wird. Er wird als gewichtetes Mittel aller möglichen Werte der Zufallsvariablen berechnet, wobei die Wahrscheinlichkeiten als Gewichte verwendet werden. Der Erwartungswert ist ein grundlegendes Maß für den „zentralen“ Wert einer Verteilung und hilft, eine allgemeine Vorstellung von den möglichen Ergebnissen eines Zufallsexperiments zu bekommen.
Die Varianz misst, wie weit die Werte einer Zufallsvariablen im Durchschnitt vom Erwartungswert entfernt sind. Eine hohe Varianz deutet darauf hin, dass die Ergebnisse stark variieren, während eine niedrige Varianz bedeutet, dass die Ergebnisse näher am Erwartungswert liegen. Die Varianz ist ein weiteres wichtiges Maß in der Stochastik, da sie Auskunft darüber gibt, wie „unsicher“ ein Zufallsexperiment ist.
Anwendungen der Stochastik
Stochastik in der Wirtschaft
In der Wirtschaft spielt die Stochastik eine zentrale Rolle bei der Analyse von Risiken und Unsicherheiten. Beispielsweise wird die Wahrscheinlichkeitstheorie verwendet, um die Preisentwicklung von Aktien zu modellieren, was für Anleger von großer Bedeutung ist. In der Finanzmathematik kommen stochastische Prozesse zum Einsatz, um zu verstehen, wie sich Finanzmärkte unter Unsicherheit entwickeln. Der Einsatz von stochastischen Modellen ermöglicht es, bessere Vorhersagen zu treffen und finanzielle Risiken zu managen.
Ein weiteres Beispiel ist die Versicherungswirtschaft, in der die Stochastik genutzt wird, um die Wahrscheinlichkeit bestimmter Schadensereignisse abzuschätzen und geeignete Prämien zu berechnen. Auch in der Wirtschaftsforschung, etwa bei der Analyse von Marktentwicklungen oder der Bestimmung von Nachfragefunktionen, sind stochastische Modelle von zentraler Bedeutung.
Stochastik in der Naturwissenschaft
In den Naturwissenschaften wird die Stochastik verwendet, um Phänomene zu modellieren, die von zufälligen Einflüssen abhängig sind. Ein Beispiel hierfür ist die Radioaktivität, bei der die Anzahl der Zerfälle eines radioaktiven Materials in einem bestimmten Zeitraum als stochastischer Prozess betrachtet wird. In der Genetik hilft die Stochastik, die Vererbung von Merkmalen und die Wahrscheinlichkeiten bestimmter genetischer Kombinationen zu verstehen.
Auch die Meteorologie ist stark von stochastischen Modellen abhängig. Die Wettervorhersage basiert auf der Modellierung von Zufallsprozessen, die viele natürliche Variablen wie Temperatur, Luftdruck und Windgeschwindigkeit berücksichtigen. Diese stochastischen Modelle sind entscheidend, um genaue Vorhersagen zu treffen und auf unvorhersehbare Änderungen des Wetters reagieren zu können.
Stochastik in der Informatik
In der Informatik spielt die Stochastik eine zentrale Rolle bei der Entwicklung von Algorithmen für maschinelles Lernen und Künstliche Intelligenz. In vielen Anwendungen, wie etwa in empfehlungssystemen, werden stochastische